Jim Shao
The phrase "Three-body" has recently gone viral in China due to the release of related novels and film/TV shows. Indeed, the three-body problem in physics is easy to let people indulge in reverie or fall into daydream because of the chaotic nature of its solution.
In 2006, out of curiosity, I studied David Acheson's book "From Calculus to Chaos"[1], which among other topics discussed the gravitational motion of three bodies in a two-dimensional plane space.
My notes are now organized as follows.
We know that if only two bodies exist, as long as the initial conditions are given, according to Newton's law, the motion trajectory and speed of the two bodies can be accurately solved.
However, in the three-body case, as shown in Figure 1, each particle is affected by the gravitational force of the other two particles. According to Newton's second law, of course, it is possible to write six second-order differential equations for motions of each particle in the X and Y directions, but these equations are coupled to each other and have no analytical solution.
Figure 1
The usual method for solution is to recast it to twelve first-order differential equations, after non-dimensionalization and then calculate it by a numerical approach, such as using the Runge-Kutta method with variable step size, in order to approximately find the instantaneous coordinates and velocity of each particle.
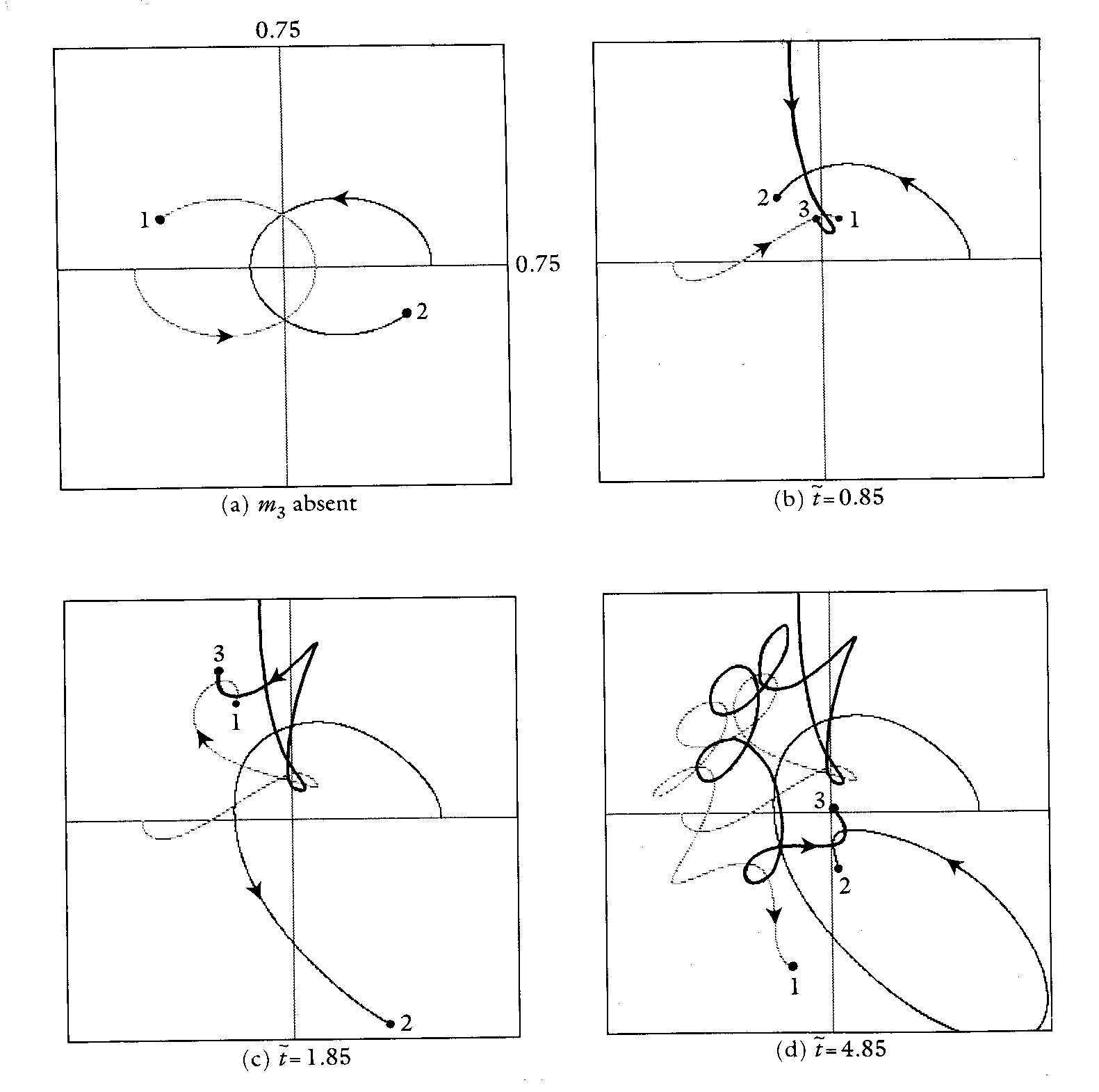
Figure 2a shows that if there is no third particle, when the masses of particles m1 and m2 are the same, equal to 0.5, the initial positions are at (0, -0.3) and (0, 0.3) points equidistant on both sides of the X-axis respectively, when the initial velocities are equal, one goes south and the other goes north, that is, (0, -0.3) and (0, 0.3), the two particles will each make a stable elliptical motion around the center of gravity of the system. This is the case with the binary star phenomenon observed in the universe.
But when a third particle intervenes, the trajectory of each particle becomes extremely complicated.
For example, m3 with the same mass enters towards south from the position of (-0.1, 0.75) with an initial velocity of (0, -0.3). As shown in Figure 2b, c, and d, particle 1 and particle 3 are quickly approaching each other and move northwest together, while particle 2 is repelled to the southeast. Soon, particle 2 returned back, entangles with particle 3, and kicks particle 1 out.
Figure 2
This mutual entanglement and constantly changing "partner" relationship can be seen more clearly in Figure 3 below. At this time, other conditions of the system are the same as Figure 2, except that the initial velocity of m3 is changed to (0, -0.2).
Figure 3
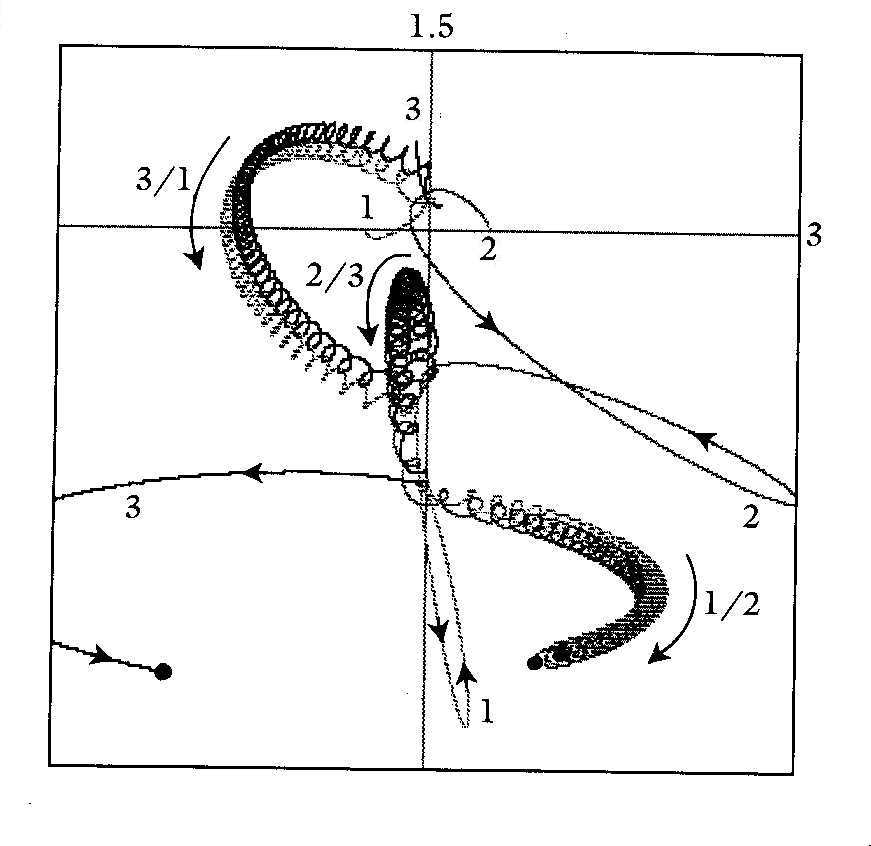
This figure shows that particle 3 and entangled particles 1 and 2 may eventually meet again. What will be happened after that?
The author followed the computer program provided in Acheson's book to further calculate the problem, and then filmed the entire process. Later, with the advice and help of a friend, I switched to screen recording technology to obtain a clearer video. Interested readers can click here: Video Link: 3-body in Motion, or http://www.azcolabs.com/3BD.mp4 to watch the video link in MP4 mode. If readers are unable to watch MP4 mode, they can try clicking the video link on the original video in AVI mode: Video Link, or http://www.azcolabs.com/3BD.avi. The short film is about three minutes long, but you may press the fast forward button in the playback software or select the playback speed to speed up the playback.
At the end of the video, it is shown that after particle 3 (black) met with particle 1 and 2 (red and green), they exchange places again. Finally, particle 2 and 3 (green and black) go together, forming something like a double star, circling each other all the way to the west, and particle 1 (red) then threw himself eastward and moved alone, similar to a rogue planet, being ejected from the binary stellar system, meandering into the abyss of space. The two groups went in opposite directions and drifted apart further and further, reaching the ending fate of three-body, decay or deconstruction and collapse.
Some readers may ask how come we haven¡¯t seen such weird behavior in the multi-body world we live in? Haven't the nine planets in the solar system been operating in an orderly manner for many years, safe and sound? Moreover, its trajectory can be predicted. People know exactly when the lunar and solar eclipses will occur, and they can also calculate the return date of Halley's Comet.
My understanding is: the three-body chaos phenomenon we are talking about here will occur, the key is that the interaction between the three bodies is of equal magnitude and affects each other, forming a strong coupling state, so that their movements are completely unpredictable.
However, if only one object has an absolute advantage in a system, such as the mass of the sun accounting for 99.86% in the solar system, many other small objects, such as planets and their satellites, will make a stable two-body motion around it. The attraction effects between these small bodies are high-order minor terms due to their small masses and long distances, and can be ignored.
At this time, if a smaller object breaks into the space between the two bodies under certain initial conditions, what will be the result?
The following four pictures illustrate this.
All the initial conditions are similar to the Figure 2, i.e. the first body (red) and the second (green) have the same mass, except the third body (black) has very small mass (m ¡Ö 0).
In the first case, as shown in Figure 4, the third body starts from a distant position (0, 10) with an initial velocity (0, -0.3), and is accelerated downward by the attraction of the two bodies. If the acceleration time is long enough for the third body to gain enough kinetic energy, or the other two bodies are at near the far end when it cuts in, it is possible for it to directly pass through the two-body system.
Figure 4
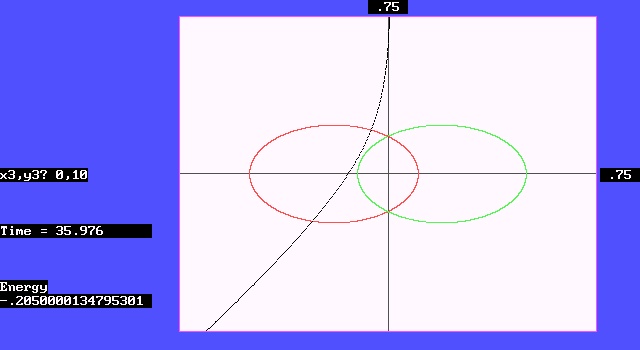
In the second case, as shown in Figure 5, the third body starts from the nearby position (0, 1) and also starts at the initial velocity (0, -0.3). Due to the short acceleration time by the attraction of the two bodies, the speed of the third body is insuffieient, and it happened to be close to the second body. As a result, it was captured by the second body and became a satellite orbiting it. However, after a considerable amount of time, the third body was freed again and flew toward the southwest.
Figure 5
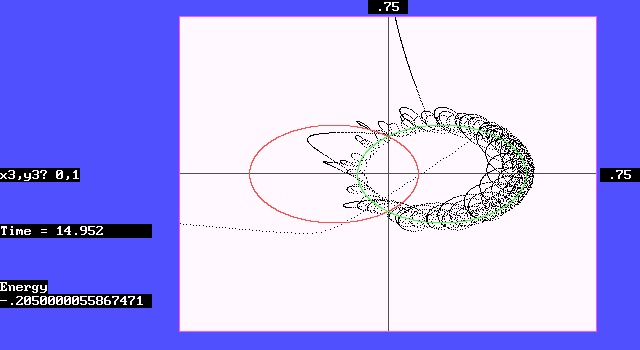
In the third case, as shown in Figure 6, the third body starts from a slightly farther position (0, 3) with the same initial velocity (0, -0.3). Due to the attraction of the two bodies, the acceleration time is slightly longer, and the third body's speed is moderate, so it was neither captured nor able to cross directly. As a result, after chaotic wandering in the potential well of the two bodies, it was finally able to escape towards about 60 degrees to the northeast.
Figure 6
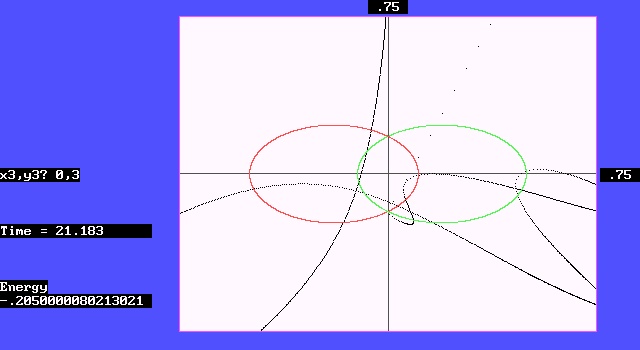
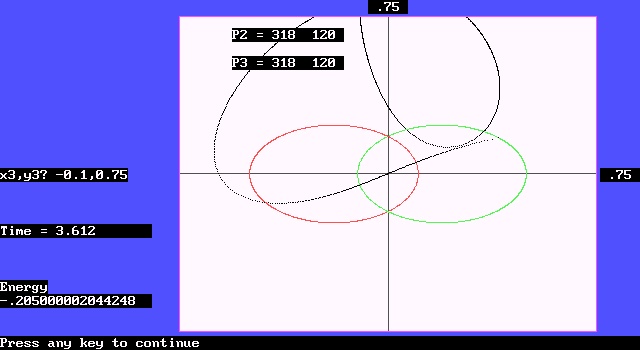
In the fourth case, as shown in Figure 7, the third body starts from the (-0.1, 0.75) position deviated from the Y-axis and also starts at the initial velocity (0, -0.3). The results are similar to the above. Only this time, it was not lucky enough to escape, but directly hit the second body. The figure shows that the position where the two particles collide is at the point of (318, 120) on the screen.
Figure 7
From the numerous craters on the moon and shooting stars seen at night on Earth, we know that such collisions are not uncommon.
The solar system has existed for billions of years, and most of the celestial bodies that should be collided or escaped have probably been eliminated. What is left now can be said to be a basically stable structure. But the laws of chaos caused by multi-body coupling still exist. From a large-scale perspective, everything may still change, including the moon quietly moving away from the earth by more than an inch every year, and countless asteroids and debris still flying around in the solar system at any time, threatening the existence of life on earth.
If we look at our Milky Way, there are estimated about 4 trillion ¡°rogue planets¡± that wander the cosmos unattached to any single stars. Their size might be from Earth to Jupiter, some of them might even have their own satellites circling around.
As illustrated above, those rogue planets were more likely ejected due to chaos from binary stellar systems than single star system.
The above are just some numerical simulations, trying to vividly illustrate some basic concepts about three-body chaotic motion and possible situations.
The vast universe is a unity of cosmos and chaos. However, in any case, three celestial bodies with similar masses are extremely unstable, and should not be suitable for the long process of the origin and evolution of life, not to mention the creation of advanced intelligent creatures.
[1], David Acheson, "From Calculus to Chaos", Oxford, (1997).
Written on April 28, 2024.
[POSTSCRIPT]
Previously, we discussed three-bodies' gravitational moving problems. The motions of this kind of systems, in general, are irregular, hardly to predict, and unstable too.
Now there is a report that once thought impossible, planets that orbit two suns, like the fictional world of Tatooine in the Star Wars franchise, have been spotted 16 times since 2011. Most of these planets orbit in the same plane as their stars.
Earlier I had only discussed the cases where the third body was entering the two-body system in a way towards its center of mass. What if the third body moves along the tangent direction at the periphery of the two-body system? Is it possible for her to be the stable common planet rotating around the two bodies?
In the following Figure, the initial conditions are the same as Figure 4 above, i.e., body 1 (red) and body 2 (green) have the same mass, the third body¡¯s (black) mass might be neglected, but it starts from the position (-1.5, 0) with an initial velocity (0, 1). The result of the simulation shows that it became the common planet around the two bodies, the orbit was quite stable although with a constant precession due to the two-body¡¯s circling each other.
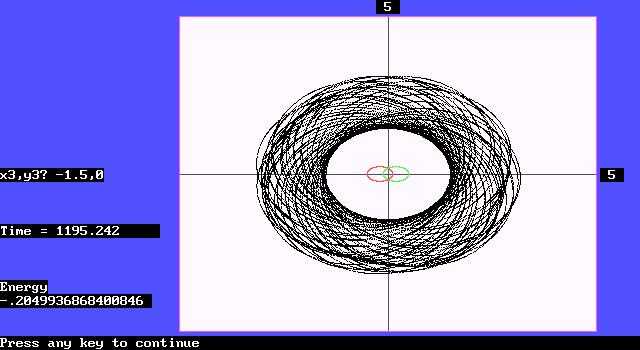
The universe is huge both in space and time, numerous ¡°rogue planets¡± had all the chances, at the proper moment and location with the proper angle and speed, to enter ¡°double star¡± systems, and became their stable planets.
So, it is realistic for planets that orbit two stars like the fictional ¡°Star Wars¡± scorching desert planet Tatooine with double sunsets that Luke Skywalker calls home.
However, a team of researchers now believes they've found a 17th ¡ª and it's the strangest yet.
A newly discovered planet named as 2M1510ABB, located about 120 light-years away. This planet orbits two smaller stars, called brown dwarfs.
Researchers found that the brown dwarfs¡¯ motion was changing ¡ª a quirk that¡¯s less likely to happen if they circled each other on their own, unless the perturbation was caused by its unseen planet nearby.
Unlike most planetary systems where planets orbit in the same plane as their stars, 2M1510ABB's orbit is probably perpendicular to the plane of the two stars, a configuration also known as a "polar orbit".
The new planet¡¯s odd orbit sets it apart. But it hasn¡¯t been directly spied, and scientists say more research is needed to be sure it¡¯s out there and figure out its mass and orbit. It is possible that the twin stars captured the rogue planet.
The following artist¡¯s illustration provided by L Calcada of the European Southern Observatory shows the possible orbit of a new exoplanet orbiting around two brown dwarfs.

The two stars that 2M1510ABB orbits are not full-fledged stars, but rather brown dwarfs, which are objects larger than planets but not massive enough to trigger nuclear fusion.
So it becomes an interesting question: if they could form a stable structure by coupling 3 mass-closed bodies in this way?
Written on April 30, 2025.
Reference
¡°Star Wars-like planet with unusual orbit found outside solar system, scientists say¡±, by ADITHI RAMAKRISHNAN, AP Science Writer, Published:9:11 AM MDT April 17, 2025.
Relevant Reading£º
Jim Shao£º"Entropy and State" (October 17, 2023)
Jim Shao£º"Langton's Ants" (August, 2017)