小 鹰

由于相关的小说和影视作品上市，最近“三体”这个词儿在中国火了。的确，物理学的三体问题，因其解的混沌性质，容易令人遐想，或墬入迷思。

2006年，出于好奇，我曾研读了大卫·艾奇逊的《从微积分到混沌》^[1]一书，其中在二维平面空间中，讨论了三体的引力运动问题。

现将笔记整理如下。

我们知道，如果只有二体存在，只要给出初始条件，根据牛顿定律，即可以精确解出二体的运动轨迹和速度。

然而，在三体情形下，如图一所示，每个粒子受到其它二粒子的引力作用，根据牛顿第二定律，固然也可以写出各粒子在X和Y方向上的六个二阶运动方程，但这些方程式彼此耦合，没有解析解。

图一

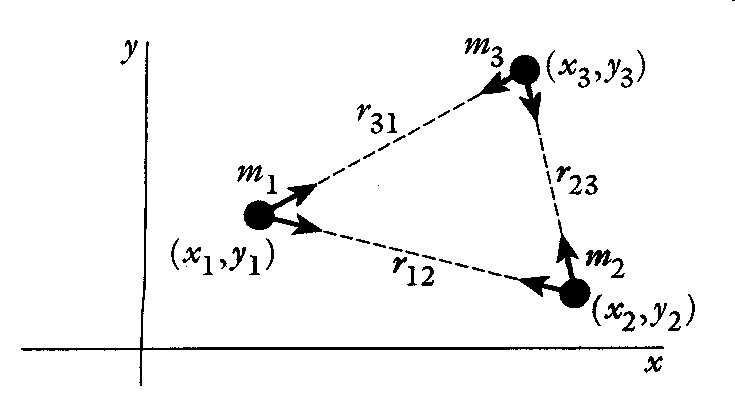
通常的求解办法是：将其降阶为十二个一阶微分方程，经去量纲化(non-dimensionalization)後，用可变步长的数字叠代法(the Runge-Kutta method)计算，近似求出每个粒子瞬时的坐标和速度。

图二a显示，如果没有第三粒子存在，当粒子m1和m2的质量相同，等于0.5，初始位置分别在X轴的两侧等距之(0，-0.3)和(0，0.3)点处，初速度大小相等，一个向南，一个向北，即为(0，-0.3)和(0，0.3)时，两个粒子将各自绕系统重心做稳定的椭圆运动。宇宙中观察到的联星或复星(binary star)现象，即是如此。

但当有第三粒子介入时，每个粒子的轨迹会变得极为复杂。

例如，具有同样质量的m3，从(-0.1，0.75)的位置，以(0，-0.3)的初速度向南进入，如图二b、c、d所示，粒子1与粒子3很快接近，一起向西北方向行，粒子2则被排斥到东南方。不久，粒子2又转回来，与粒子3缠绕，把粒子1踢了出去。

图二

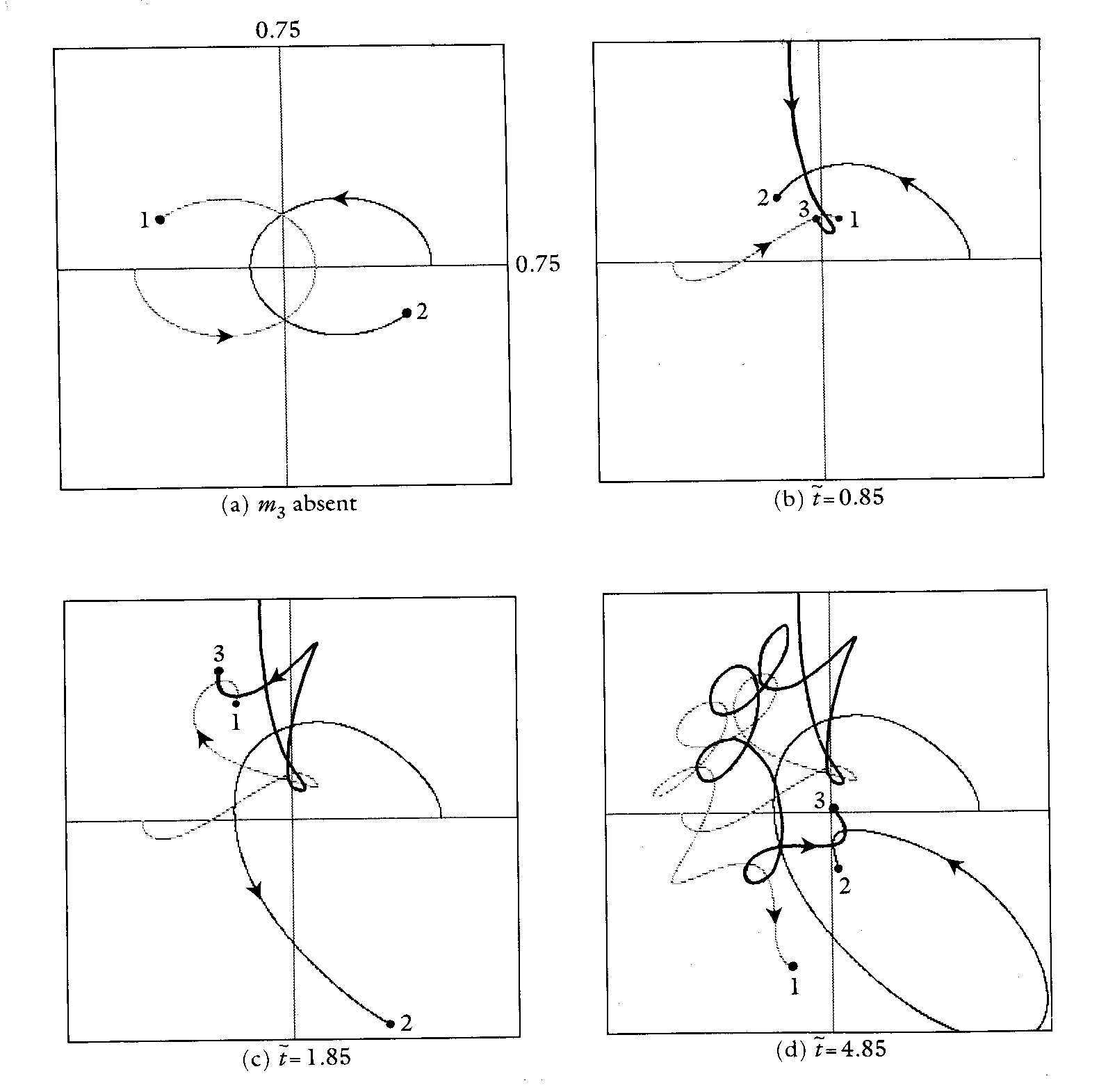
这种相互纠缠，不断变换“伙伴”的关系，在下面的图三中可以看得更清楚，此时系统其它条件与图二相同，只是m3的初速改为(0，-0.2)。

图三

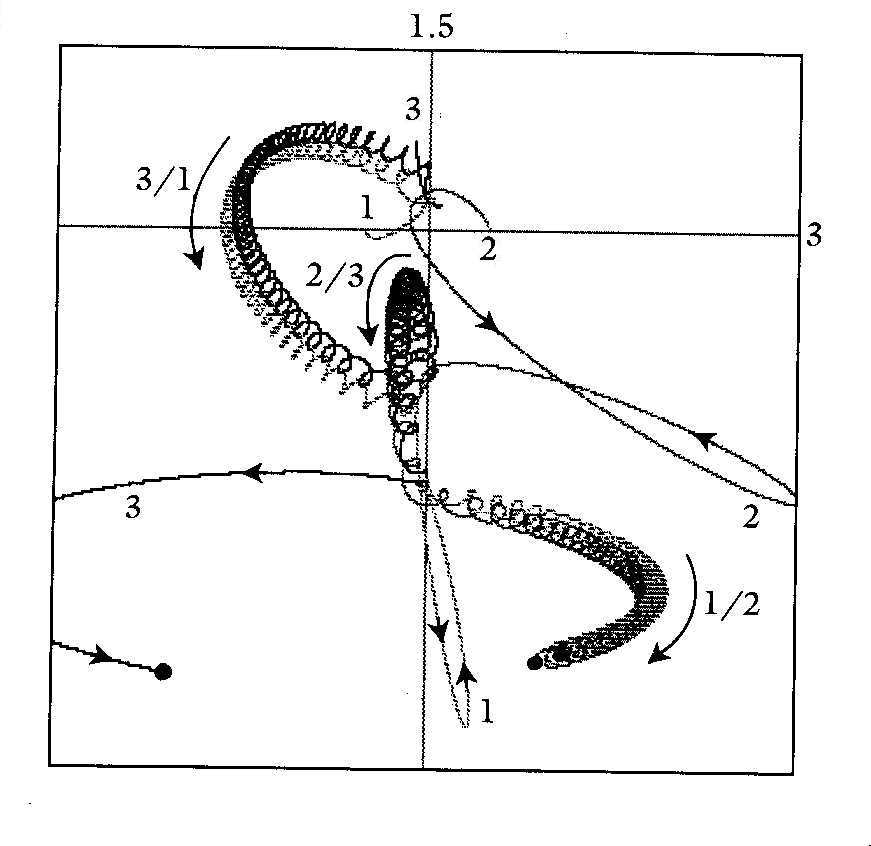
该图显示，粒子3与彼此纠缠的粒子1和2最後可能再次相遇，那之後的结果又会是怎样？

笔者按照Acheson书中提供的程序，进一步演算，并将全过程拍成影片，後经友人建议和帮助，又改用录屏技术，获得更清晰的视频。有兴趣的读者可以点击这里观看：MP4模式的视频链接：三体动态图。如有读者无法观看MP4模式，可试点击AVI模式的原摄影片视频链接。该短片长约三分钟，但可按播放软件中的快进键或选择播放速度，加快播放。

影片结尾时显示，粒子3(黑)与粒子1/2(红与绿)相会之後，再次交换位置，最终，粒子2/3(绿与黑)结伴，类似一对双星(double star)，彼此绕行，一路向西，粒子1(红)则形同一颗脱离联星的“流浪行星”(a rogue planet)，在太空深渊中独自投东，踽踽而行。二者背道而驰，渐行渐远，达到了三体衰变(decay)或解构崩溃的结局。

有些读者可能会问，在我们生活的多体大千世界，怎麽没有见过如此诡异的行径？太阳系的九大行星不是秩序井然地运行多年，安然无恙麽？而且轨迹可以预测，人们准确知道月蚀、日蚀会在什麽时候发生，也可推算出哈雷彗星回归的日子。

我的理解是：我们这里说的三体混沌现象会发生，关键在于三体间的相互作用量级相当，彼此影响，形成强耦合状态，以致其运动完全无法预测。

但是，如果一个体系，只有一个物体占绝对优势，如太阳系中太阳的质量占99.86%，其余众多小物体，如诸行星及其卫星，则各自围绕它做稳定的二体运动；至于行星彼此间的吸引，由于质量小且相距较远，属于高阶小项微扰，可能会引起行星的些许进动，或者可以忽略不计。

此时，若有更小的物体，以一定的初始条件，闯入二体之间，结果会怎么样？

以下四张图片，对此做了说明。

初始条件与图二相似，即：一、二体(红与绿)质量相同，只是第三体(黑)质量很小(m ≈ 0)。

第一种情形，如图四显示，第三体从远处(0，10)的位置，以初速(0，-0.3)出发，受二体的吸引加速向下。如果加速时间够长，使第三体获得足够的动能，或当切入时另二体恰在远端附近，那它就有可能直接穿越二体体系。

图四

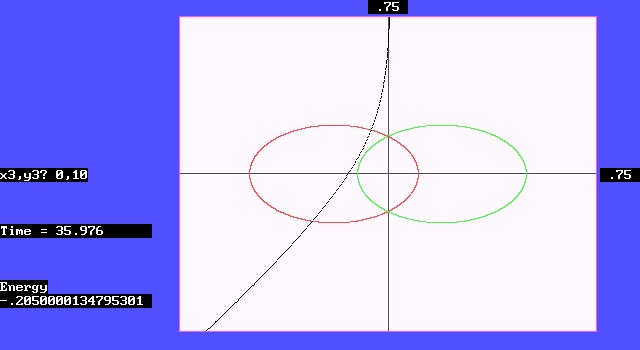
第二种情形，如图五显示，第三体从近处(0，1)的位置，同样以初速(0，-0.3)出发，因受二体吸引加速时间较短，第三体速度不够高，且刚好与第二体接近，结果被第二体俘获，成为绕其旋转的卫星。然而，经过相当的时间之後，第三体又解脱出来，向西南方向飞去。

图五

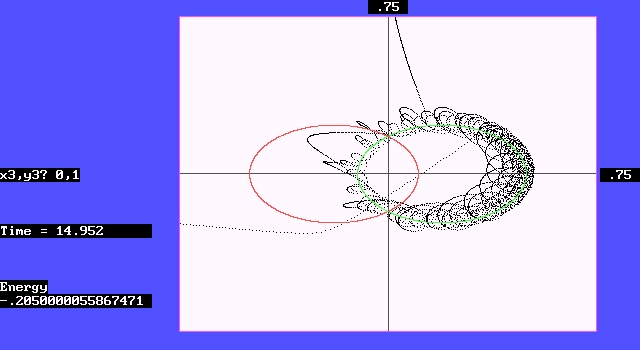
第三种情形，如图六显示，第三体从稍远的(0，3)位置，同样以初速(0，-0.3)出发，因受二体吸引加速时间略长，第三体速度居中，它既不被俘获，又无力直接穿越，结果在二体的势井中，混沌漫游一番之後，终于得以向东北约60度方向逃逸。

图六

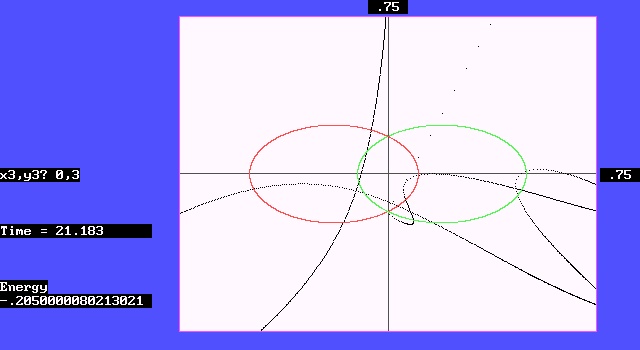
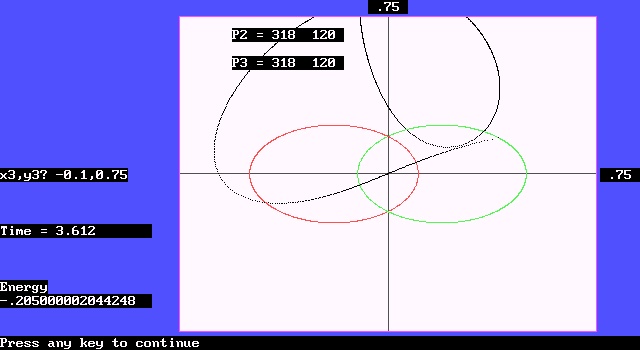
第四种情形，如图七显示，第三体从偏离Y轴的(-0.1，0.75)位置，同样以初速(0，-0.3)出发，结果与上相似。只是这一次，它没能幸运逃逸，而是直接撞上了第二体。图中显示二粒子相撞的位置在屏幕的(318，120)点处。

图七

从月球上的无数陨石坑和地球上夜间常见到的流星，可知这种相撞情形并不罕见。

太阳系存在已有几十亿年，该撞的或能逃的天体大概多已被淘汰了，现在剩下的，可以说，是一个基本稳定的结构。但多体耦合导致的混沌法则依然存在，从大尺度来看，一切仍旧可能改变，包括月球每年正悄悄地远离地球约一英寸多，无数小行星和碎石块仍在太阳系里杂乱飞舞，随时威胁着地球上的生命存在。

而放眼银河系，那里大约有4万亿个不隶属于任何恒星的“流浪行星”(the rogue planets)在星际空间中游荡，其大小如地球到木星不等，有些还带有自己的卫星环绕。

如前文所述，这些流浪行星很可能是从联星或复星天体系统(binary stellar systems)中因混沌被排斥出来的。

以上只是些数字模拟，试图形象地给出有关三体混沌运动中的一些基本概念，以及可能发生的情形。

浩瀚的宇宙是和谐秩序与紊乱混沌的统一体，然而，无论如何，质量相近的三体天体极不稳定，应不适合生命起源和进化的漫长过程，遑论产生造就高级智慧生物。

[1], David Acheson, "From Calculus to Chaos", Oxford, (1997).

写于2024年4月28日。

To read English version please click: Jim Shao, “The three-body problem”

Or, goto http://www.azcolabs.com/xy_3BD_Eng.html

[後记]

前文在二维平面空间中，讨论了三体的引力运动问题。通常认为，这种系统的运动不规则，难以预测，也不稳定。

最近看到报导，自2011年以来，人们已有16次观察到有行星围绕双星(double star)运行的事例，其行星的轨道多与双星运动处于同一平面。

这一事实提醒了笔者，前文只讨论了第三体──无论其质量与二体相当或可忽略不计──在同一平面中朝二体质心方向垂直进入时的几种可能的後果，即：导致三体解构，或穿越、被俘获、逃逸和碰撞等。

但如果质量微小的第三体，一开始是沿二体外围切线方向运动，那它是否有可能成为彼此绕行的二体共同的行星呢？

下图中，初始条件与图四相同，即：一、二体(红与绿)质量相同，第三体(黑)质量很小(m ≈ 0)，只是第三体于(-1.5，0)处，以初速(0，1)出发。计算模拟的结果显示，它成为二体的共同行星，尽管其轨道受二体运动影响不断进动，但相当地稳定。

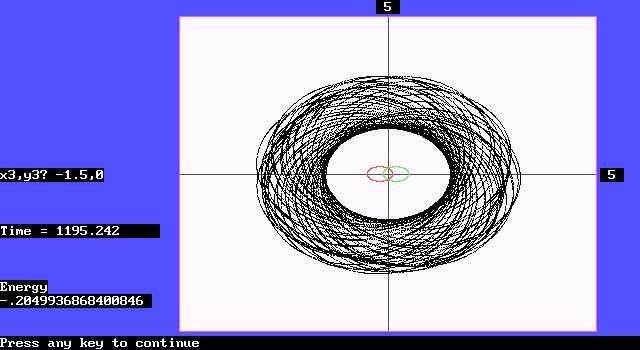
宇宙浩瀚，无数“流浪行星”有各种机会，在适当的时刻和地点，以合适的角度与速度，进入双星体系，在同一平面内成为它们稳定的行星。因此，科幻电影“星际大战”中，那个有着两个太阳的行星，是完全有可能存在的。

然而，2025年4月美联社报道，科学家在120光年处发现了由一对褐矮星(brown dwarfs)组成的双星(2M1510AB)，其彼此绕行的轨迹不同寻常地古怪。研究者猜测，这可能是由于有一颗轨道与双星平面垂直，称为“极性轨道”("polar orbit")，的行星干扰的结果，尽管这颗行星还未被直接观察到，其质量与轨道均有待进一步的研究决定，而它的来源亦很可能是被该双星俘获的一颗星际流浪行星。

下面是欧洲南方天文台(the European Southern Observatory)L Calcada对该三体运动所绘制的艺术印象图。

褐矮星的质量大于行星，但又不足以引起核聚变。因此，由三个质量相近的天体的如此耦合，能否形成一种稳定的结构？这是一个有趣的问题。

记于2025年4月30日。

参考资料

Star Wars-like planet with unusual orbit found outside solar system, scientists say，by ADITHI RAMAKRISHNAN，AP Science Writer，Published:9:11 AM MDT April 17, 2025

链接网站首页-阅读更多内容